Graphic Quadratic Functions in Vertex or Intercept Form:
Vertex Form:
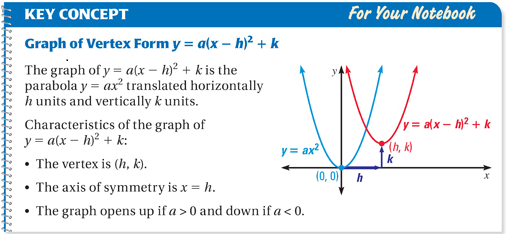
Quadratic functions can be written in vertex form, or y = a(x-h)^2 + k; this form shows the position of the function
f(x) = ax^2, after being translated h units horizontally and k units vertically. This is especially useful because the vertex of the function is found at the point (h, k).
f(x) = ax^2, after being translated h units horizontally and k units vertically. This is especially useful because the vertex of the function is found at the point (h, k).
Intercept form:
*NOTE: This only applies when the function has at least one x-intercept, you have been warned.....*
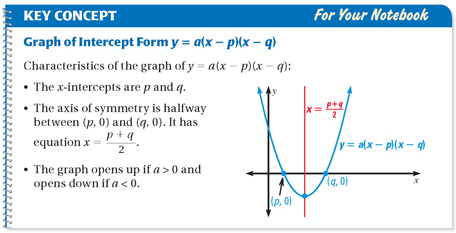
A quadratic function can also be written as y=a(x - p)(x - q), or intercept form; this is helpful because both p and q are the x-intercepts of the function, and the axis of symmetry for the function can be found using the equation x=(p + q)/2.
A quadratic function can also be written as y=a(x - p)(x - q), or intercept form; this is helpful because both p and q are the x-intercepts of the function, and the axis of symmetry for the function can be found using the equation x=(p + q)/2.